数据预处理——3sigma 原则离群值处理

原文： https://zhuanlan.zhihu.com/p/403203117

在统计上，68–95–99.7 原则是在正态分布中，距平均值小于一个标准差、二个标准差、三个标准差以内的百分比，更精确的数字是 68.27%、95.45% 及 99.73%。若用数学用语表示，其算式如下，其中 X 为正态分布随机变数的观测值，μ为分布的平均值，而σ为标准差：

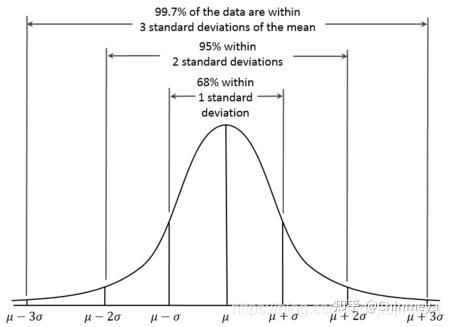
3sigma 又称为标准差法。标准差本身可以体现因子的离散程度，是基于因子的平均值 Xmean 而定的。在离群值处理过程中，可通过用 X_(mean)\pm n\sigma 来衡量因子与平均值的距离。标准差法处理的逻辑与 MAD 法类似，首先计算出因子的平均值与标准差，其次确认参数 n，从而确认因子值的合理范围为 [X_(mean)- n\sigma,X_(mean)+ n\sigma]，并对因子值作的调整。

该原理一般在工程科学中比较常用。3sigma 原理可以简单描述为：若数据服从正态分布，则异常值被定义为一组结果值中与平均值的偏差超过三倍标准差的值。即在正态分布的假设下，距离平均值三倍 \sigma（标准差）之外的值出现的概率很小（如下式)，因此可认为是异常值。

P(|x-\mu|>3\sigma)\leq0.003 \

若数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述（这就使该原理可以适用于不同的业务场景，只是需要根据经验来确定 k sigma 中的 k 值，这个 k 值就可以认为是阈值）。

代码如下：

#-*- coding: utf-8 -*-
#基于3sigma的异常值检测
​
def tupleSigma(path):
    #path --> data path
    n = 3
    data = pd.read_excel(path, index_col = False) #读取数据
    data_y = data[u'销量']
    data_x = data[u'日期']
​
    ymean = np.mean(data_y)
    ystd = np.std(data_y)
    threshold1 = ymean - n * ystd
    threshold2 = ymean + n * ystd
​
    outlier = [] #将异常值保存
    outlier_x = []
​
    for i in range(0, len(data_y)):
        if (data_y[i] < threshold1)|(data_y[i] > threshold2):
            outlier.append(data_y[i])
            outlier_x.append(data_x[i])
        else:
            continue
​
    print('\n异常数据如下：\n')
    print(outlier)
    print(outlier_x)
​
    plt.plot(data_x, data_y)
    plt.plot(outlier_x, outlier, 'ro')
    for j in range(len(outlier)):
        plt.annotate(outlier[j], xy=(outlier_x[j], outlier[j]), xytext=(outlier_x[j],outlier[j]))
    plt.show()